numpy.ma.polyfit#
- ma.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)[原始碼]#
最小平方法多項式擬合。
注意
這是舊多項式 API 的一部分。自 1.4 版以來,建議使用在
numpy.polynomial中定義的新多項式 API。差異摘要請見轉換指南。將 deg 次多項式
p(x) = p[0] * x**deg + ... + p[deg]擬合到點 (x, y)。傳回係數向量 p,其以 deg、deg-1、… 0 的順序最小化平方誤差。建議新程式碼使用
Polynomial.fit類別方法,因為它在數值上更穩定。詳情請參閱該方法的文檔。- 參數:
- xarray_like,形狀 (M,)
M 個樣本點
(x[i], y[i])的 x 座標。- yarray_like,形狀 (M,) 或 (M, K)
樣本點的 y 座標。可以一次擬合多個共享相同 x 座標的樣本點資料集,方法是傳入一個 2D 陣列,其中每欄包含一個資料集。
- degint
擬合多項式的次數
- rcondfloat,選用
擬合的相對條件數。相對於最大奇異值,小於此值的奇異值將被忽略。預設值為 len(x)*eps,其中 eps 是浮點類型的相對精度,在大多數情況下約為 2e-16。
- fullbool,選用
決定傳回值性質的開關。當為 False(預設值)時,僅傳回係數;當為 True 時,也會傳回來自奇異值分解的診斷資訊。
- warray_like,形狀 (M,),選用
權重。如果不是 None,則權重
w[i]適用於x[i]處的未平方殘差y[i] - y_hat[i]。理想情況下,選擇權重是為了使乘積w[i]*y[i]的誤差都具有相同的變異數。當使用逆變異數權重時,請使用w[i] = 1/sigma(y[i])。預設值為 None。- covbool 或 str,選用
如果給定且不為 False,則不僅傳回估計值,還傳回其共變異數矩陣。預設情況下,共變異數會按 chi2/dof 縮放,其中 dof = M - (deg + 1),即權重被假定為不可靠,除非在相對意義上,並且所有內容都經過縮放,使得縮減的 chi2 為 unity。如果
cov='unscaled',則會省略此縮放,這與權重為 w = 1/sigma 的情況相關,其中 sigma 已知是不確定性的可靠估計。
- 傳回值:
- pndarray,形狀 (deg + 1,) 或 (deg + 1, K)
多項式係數,最高次項優先。如果 y 是 2D 陣列,則第 k 個資料集的係數位於
p[:,k]中。- residuals、rank、singular_values、rcond
只有在
full == True時才會傳回這些值residuals – 最小平方法擬合的平方殘差和
- rank – 縮放的 Vandermonde 矩陣的有效秩
係數矩陣
- singular_values – 縮放的 Vandermonde 矩陣的奇異值
係數矩陣
rcond – rcond 的值。
如需更多詳細資訊,請參閱
numpy.linalg.lstsq。- Vndarray,形狀 (deg + 1, deg + 1) 或 (deg + 1, deg + 1, K)
僅當
full == False且cov == True時存在。多項式係數估計的共變異數矩陣。此矩陣的對角線是每個係數的變異數估計值。如果 y 是 2D 陣列,則第 k 個資料集的共變異數矩陣位於V[:,:,k]中
- 警告:
- RankWarning
最小平方法擬合中係數矩陣的秩不足。僅當
full == False時才會引發警告。可以透過以下方式關閉警告
>>> import warnings >>> warnings.simplefilter('ignore', np.exceptions.RankWarning)
另請參閱
polyval計算多項式值。
linalg.lstsq計算最小平方法擬合。
scipy.interpolate.UnivariateSpline計算樣條擬合。
註解
x 中的任何遮罩值都會在 y 中傳播,反之亦然。
此解最小化了平方誤差
\[E = \sum_{j=0}^k |p(x_j) - y_j|^2\]在方程式中
x[0]**n * p[0] + ... + x[0] * p[n-1] + p[n] = y[0] x[1]**n * p[0] + ... + x[1] * p[n-1] + p[n] = y[1] ... x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]
係數 p 的係數矩陣是 Vandermonde 矩陣。
polyfit在最小平方法擬合條件不佳時會發出RankWarning。這表示由於數值誤差,最佳擬合未明確定義。可以透過降低多項式次數或將 x 替換為 x - x.mean() 來改善結果。rcond 參數也可以設定為小於其預設值的值,但產生的擬合可能是虛假的:包含來自小奇異值的貢獻可能會將數值雜訊添加到結果中。請注意,當多項式的次數很大或樣本點的間隔未良好居中時,擬合多項式係數在本質上是條件不佳的。在這些情況下,應始終檢查擬合的品質。當多項式擬合不令人滿意時,樣條曲線可能是很好的替代方案。
參考文獻
[1]Wikipedia, “曲線擬合”, https://en.wikipedia.org/wiki/Curve_fitting
[2]Wikipedia, “多項式插值”, https://en.wikipedia.org/wiki/Polynomial_interpolation
範例
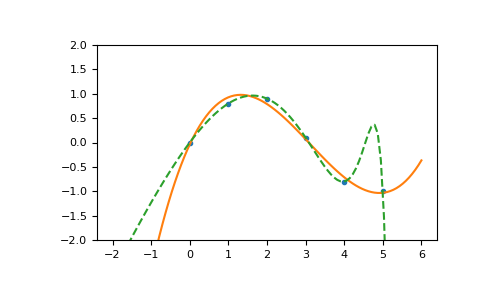
>>> import numpy as np >>> import warnings >>> x = np.array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0]) >>> y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0]) >>> z = np.polyfit(x, y, 3) >>> z array([ 0.08703704, -0.81349206, 1.69312169, -0.03968254]) # may vary
使用
poly1d物件處理多項式很方便>>> p = np.poly1d(z) >>> p(0.5) 0.6143849206349179 # may vary >>> p(3.5) -0.34732142857143039 # may vary >>> p(10) 22.579365079365115 # may vary
高階多項式可能會劇烈震盪
>>> with warnings.catch_warnings(): ... warnings.simplefilter('ignore', np.exceptions.RankWarning) ... p30 = np.poly1d(np.polyfit(x, y, 30)) ... >>> p30(4) -0.80000000000000204 # may vary >>> p30(5) -0.99999999999999445 # may vary >>> p30(4.5) -0.10547061179440398 # may vary
圖例
>>> import matplotlib.pyplot as plt >>> xp = np.linspace(-2, 6, 100) >>> _ = plt.plot(x, y, '.', xp, p(xp), '-', xp, p30(xp), '--') >>> plt.ylim(-2,2) (-2, 2) >>> plt.show()